These Mysterious Shapes Are at the Heart of Math’s Biggest Puzzles

When most people think of shapes, they imagine a triangle, a rectangle, or maybe even a fancier- sounding rhombus or trapezoid. But to mathematicians, shapes encompass a vast universe of surprising forms, from one-dimensional loops to polytopes (geometric objects with flat sides that can exist in any desired dimension).

A related category, surfaces—collections of points that form boundaries in 3D space—includes an entire zoo of striking, strange mathematical objects. In this playground of structures and ideas, mathematicians explore, discover new insights and ponder open questions.

Some mathematicians love shapes that are deeply connected to the physical world, such as Borromean rings, which are related to regular hair braids, and the permutahedron, which is the basic shape of a zeolite crystal (a material widely used in industrial applications). Others favor more abstract options that represent higher-dimensional realms seemingly divorced from the world we live in.

On supporting science journalism

If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

We asked mathematicians to choose their favorite shapes and surfaces and tell us why they find them so exciting and intriguing. Here are their edited responses.

The Loop

My favorite shape is the loop, a circle with all geometric information stripped away, leaving only a free-form one-dimensional object. In fact, there’s a sense in which it is the only one-dimensional object. The biggest questions in topology [the branch of math concerned with the properties of shapes that stay constant even when the forms are stretched and warped] concern classifications of closed manifolds, which are the abstract notion of what “shape” means to a topologist. Surprisingly, we have a good sense of what every possible closed manifold looks like, provided it is one-, two- or three-dimensional or five-or-more-dimensional, but we know little about how four-dimensional manifolds can look. In this framework, the only one-dimensional closed manifold is a loop.

The loop is also ubiquitous throughout different fields of topology, often in a very crucial way. For example, the most fruitful and important invariant in topology is arguably the fundamental group, an algebraic object that counts how many ways a loop can be squeezed inside a space. And knot theory is an entire field of math focusing on the question “What are all the ways a loop can be tangled in three-dimensional space?” There is still so much to be learned about loops. —Shintaro Fushida-Hardy, Stanford University

The Complement of a Knot

The complement of a knot is everything in three-dimensional space that isn’t the knot. It’s a topological object—if you wiggle the knot around, then its complement also squishes around. In the late 1970s American mathematician Robert F. Riley realized the complement of the figure-eight knot—this flexible topological object—is secretly an impossibly hard geometric diamond.

This is all metaphor—by “geometric diamond,” I mean it isn’t just topological; it has geometry to it, and “diamond” is supposed to make you think of a rigid gemstone. It is a gem, as in a singular, beautiful object, and it is rigid in the sense that you cannot change its geometry—the geometry is unique. “Impossibly hard” is also trying to express this rigidity.

Riley showed that the complement of the figure-eight knot has a complete hyperbolic metric—in fact, a unique such metric. [“Hyperbolic” refers to a hyperbola, an open-ended curve.] This means that, for example, it makes sense to ask what its volume is given this unique metric. (It holds approximately 2.03 units of hyperbolic volume.) Soon after, mathematician William Thurston, then at Princeton University, vastly extended Riley’s insight, showing that in a certain sense almost all knots have hyperbolic complements. Of the 352,152,252 prime knots with up to 19 crossings (classified by Benjamin A. Burton of the University of Queensland in Australia), only 395 are not hyperbolic.

What’s a prime knot? Natural numbers are either composite or prime, depending on whether you can factor them into smaller pieces that then multiply together to give the number you started with. There is a similar situation with knots—instead of multiplication to combine two numbers to make a bigger number, an operation called connect sum combines two knots into a single, bigger knot. A knot is prime if it is not composite—that is, if it cannot be made by summing two smaller knots. People usually care only about prime knots because you can usually understand any composite knot by breaking it up into its prime knot factors first. —Henry Segerman, Oklahoma State University

Hyperbolic Pair of Pants

My favorite shape—and one I think about every day—is called the hyperbolic pair of pants. It is a surface with the shape of a pair of pants, meaning it has three boundary components (a waist and two ankles) and genus 0 (no handle, as opposed to your coffee mug). What makes this shape so special is that to every three lengths a, b and c, we can associate one and only one hyperbolic pair of pants of boundary lengths a, b and c. Thus, the same way that you know how to draw “the rectangle of edges 2 and 3.5,” it makes sense to talk about “the hyperbolic pair of pants of boundaries 1, 6 and 2.4.”

You can play and sew hyperbolic pairs of pants together. When you sew two pairs of jeans along their beltlines, an important decision is whether to line up their buttons and, if not, how much to twist. The amount of twisting is called the twist angle, represented by tau (τ). We can construct every hyperbolic surface by sewing together hyperbolic pairs of pants and describe all of them entirely in terms of the boundary lengths and twist angles in this decomposition. Therefore, hyperbolic pairs of pants are the perfect building blocks of hyperbolic geometry. — Laura Monk, University of Bristol, England

Polytopes

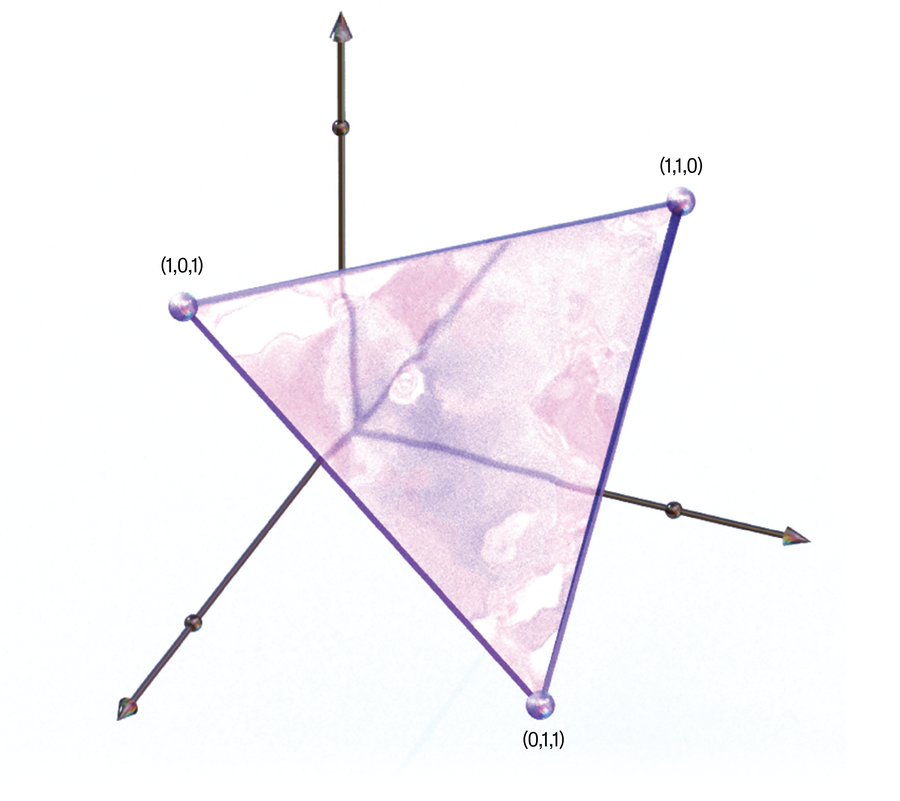
The shapes I continue to return to in my research career are both commonplace and complex. They are commonplace because we learn about two-dimensional versions of these shapes as children: triangles, squares, dodecahedrons, and other convex polygons [a polygon is any flat shape made with straight lines; a convex polygon has internal angles that are all less than 180 degrees]. They become complex quickly as one considers higher-dimensional versions of them, called polytopes, and recognizes the myriad pure and applied mathematical connections they have. For example, if one has tried to optimize a bounded linear system (for example, to minimize the time required to return electric bikes to their rental stations), then one has encountered a polytope. If one is able to encode data from one mathematical setting as 0/1 coordinates, then the convex hull of those points [the smallest convex shape enclosing the points] describes a polytope. For example, the set of subsets of size 2 over three elements produces the three coordinate points (1,1,0), (1,0,1) and (0,1,1), whose convex hull is a triangle in three-dimensional space. This approach opens up a world of mathematical possibilities and deepens connections between mathematical areas. What may be hard to state in one area may suddenly be easier to state using polytopal language. It is these kinds of relationships between various mathematical areas, as well as the pursuit of exploring polytopes in their own right, that keep my attention on these simple yet complicated shapes. —Anastasia Chavez, Saint Mary’s College of California

Permutahedron

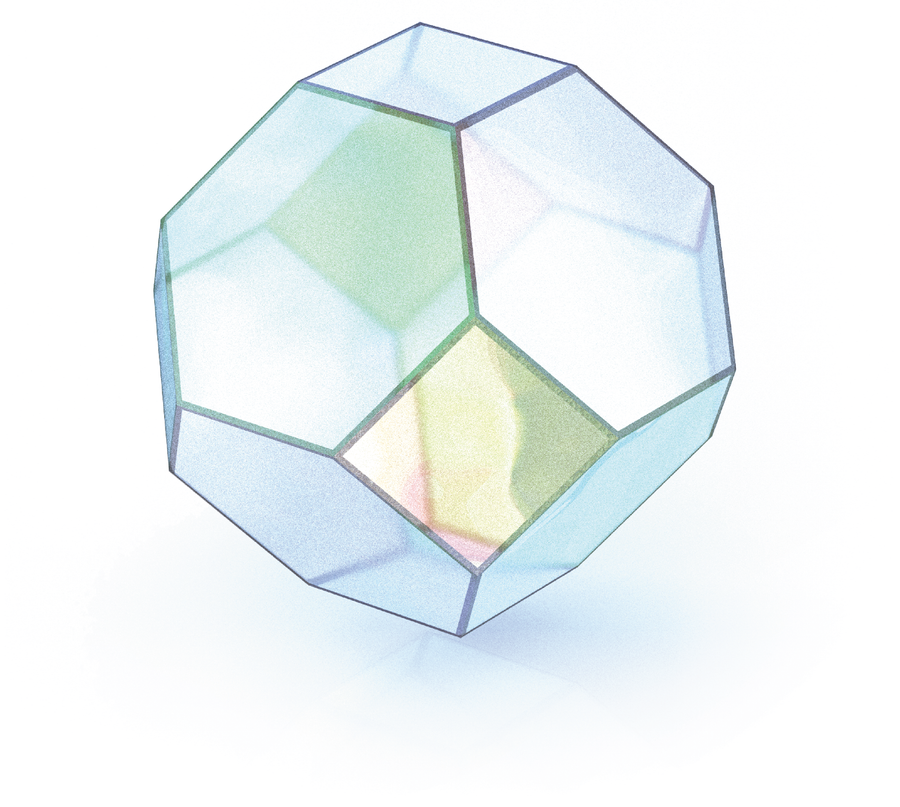
One shape that I find really cool is known as the permutahedron (sometimes spelled permutohedron). This is a very symmetrical convex polytope that exhibits many special properties.

First, what does it mean for a shape to be convex? Think of it like this: if you pick any two points inside the shape and draw a straight line between them, that line will always stay inside the shape.

Second, what is a convex polytope? A convex polytope can be thought of as a shape with flat sides that may exist in any dimension: the zero-dimensional polytopes are points, the one-dimensional polytopes are line segments, and the two-dimensional polytopes are polygons. In three dimensions, we have polyhedra; in general, we have d-polytopes for any dimension d. For example, I like to think about convex polytopes in three dimensions as taking some points, throwing them in space and then sealing them in plastic wrap as tightly as you can. As a result, you will get a three-dimensional shape with flat sides. In two dimensions, we can think about points being represented by the heads of nails, wrapping a rubber band around the nails and letting the rubber band snap, creating a polygon.

Now, what is the permutahedron? The n-permutahedron is a geometric shape that comes from the mathematical concept of permutations. Say you have a set of numbers 1, 2 and 3. You can arrange those three numbers in different orders: (1,2,3), (1,3,2), (2,3,1), and so on. These different orders are called permutations. The n-permutahedron is a shape that captures all the possible ways to arrange the numbers 1 through n (for a positive integer n). We can define the n-permutahedron as the convex hull of all permutations of the vector (1,2,…,n).

When n = 3, we have six permutations of (1,2,3), which are the vertices of the 3-permutahedron. It is important to note that the 3-permutahedron is a two-dimensional figure “living” in 3-space. The reason behind this is that all the permutations (thought of as points in 3-space) live on the plane where x + y + z = 6, thus bringing down the dimension of the polytope.

See, for example, the 4-permutahedron. When n = 4, we have 4! = 24 permutations of (1,2,3,4), which are the vertices of the 4-permutahedron, a 3D polytope that lives in 4-space. This polytope is actually a truncated octahedron, a shape with 14 sides (six squares and eight regular hexagons). And truncated octahedra can create a space-filling tiling of 3-space. —Andrés R. Vindas Meléndez, Harvey Mudd College

You might have seen this beautifully symmetrical shape in your neighborhood playground; my chemist friend Juliana Velasquez Ochoa of the University of Bologna tells me it is the basic shape in a zeolite crystal. The San Francisco Exploratorium has a pile of identical bright-red permutahedra; when you play with them, you quickly notice that they stack perfectly, tiling [filling] space with no empty space between them.

How do we place 24 vertices in space to make the permutahedron Π₄? My favorite way is to place them in four-dimensional space. The vertices of Π₄ are the 4! = 4 × 3 × 2 × 1 = 24 orderings (1,2,3,4), (2,1,3,4),…, (4,3,2,1) of the numbers 1,2,3,4. The volume of the permutahedron Π₄ is 32 = 4^4–2√4; we know this because Π₄ is a shadow of the 4(4 – 1)/2 = 6-dimensional cube, and this fact gives us a way to cut up the permutahedron Π₄ into 16 = 4^4–2 identical boxes of volume √4.

The best part of this story is that it is true in any dimension. You can just substitute any value n instead of the number 4. (Why don’t you try it for n = 3?) The vertices of the permutahedron Π_n correspond to the possible orders of n objects. So as I alphabetize the stack of final projects of my 18 combinatorics students, I am taking a stroll around Π₁₈ in 18-dimensional space.

I love the permutahedron because it is the site of a beautiful, productive dialogue among geometry, algebra and combinatorics [the study of counting, permutations and combinations]. —Federico Ardila-Mantilla, San Francisco State University

The Loch Ness Monster Surface

As someone who studies surfaces for a living, I find it hard to pick a favorite. A common joke in my research area is that everyone’s favorite surface is the genus 2 surface [a surface with two holes in it] because it’s the lowest-genus (closed) hyperbolic surface and, as such, is often the default example drawn in lectures and talks. Although the genus 2 surface is quite special, I decided to share a little bit about a surface on the other end of the spectrum, an infinite-genus surface called the Loch Ness monster. The Loch Ness monster surface is arguably the “simplest” infinite-type surface, yet its group of topological symmetries known as the mapping class group contains every countable group as a subgroup.

Even stronger, there exists a complete hyperbolic metric on the Loch Ness monster surface whose isometry group (the group of geometric symmetries) is G if and only if G is a countable group. So even though the Loch Ness monster surface may appear quite simple in the wild world of infinite-type surfaces, it captures some pretty neat phenomena. These cool facts were proved by Tarik Aougab of Haverford College, Priyam Patel of the University of Utah and Nicholas G. Vlamis of Queens College in New York City in a 2021 paper entitled “Isometry Groups of Infinite-Genus Hyperbolic Surfaces.” —Marissa Kawehi Loving, University of Wisconsin–Madison

2D Real Projective Space

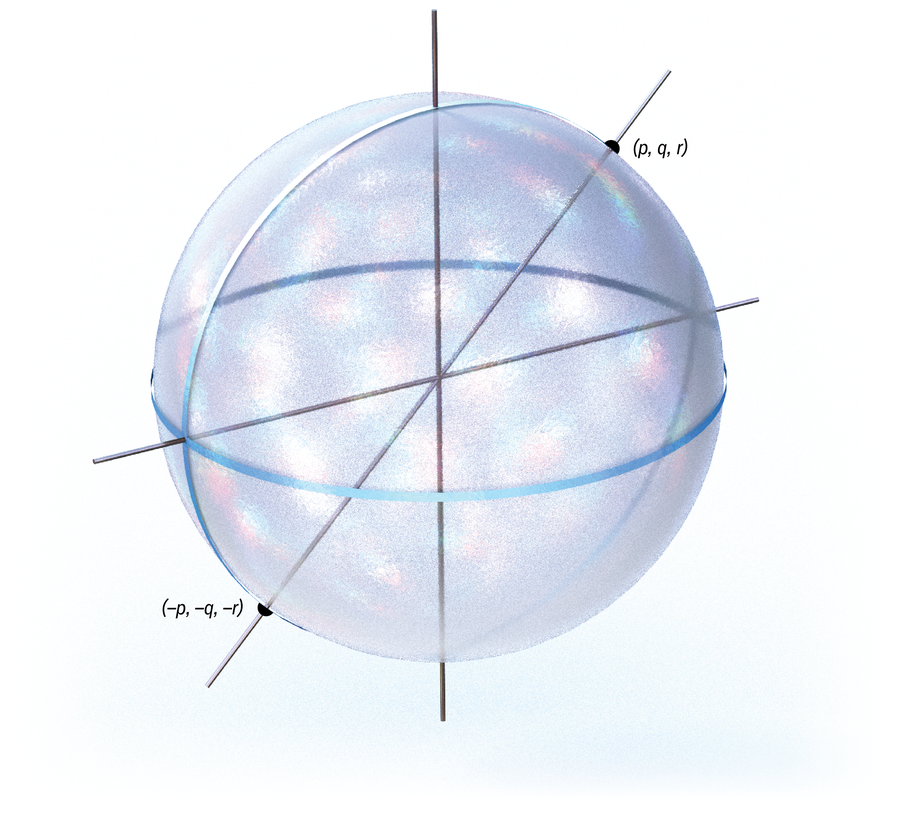
I’m a topologist, so I’m enthusiastic about a lot of surfaces and shapes, but probably my favorite surface in the sense of a two-dimensional manifold [a surface that behaves like regular space at the local level] is ℝℙ², or two-dimensional real projective space. In general, ℝℙⁿ is the set of lines through the origin in ℝⁿ⁺¹. So for ℝℙ², we’re looking at all the lines through the origin in ℝ³; we can think of it like all the points on the unit sphere, except that any time two points are exactly opposite each other, we treat them as the same because they are on the same line through the origin. This surface can also be thought of in the following way: Take a Mobius band [essentially a strip of paper twisted once with its ends attached] and a disk. Both those things have a boundary, or edge: a circle. If we glue those two boundary circles together, we get two-dimensional real projective space.

This surface is the first step in an important construction in topology, which is to take the set of lines in all spaces ℝⁿ, for any dimension n, at the same time. (Equivalently, you can take the set of lines in ℝ^∞. This space, called ℝℙ^∞, has deep connections to many features of topology I like, such as realizing fairly abstract algebraic invariants in terms of maps between spaces, studying vector fields on manifolds and studying the behavior of simple symmetries on spaces. —Kristen Hendricks, Rutgers University

Curves That Shaped William W. S. Claytor’s Mathematics

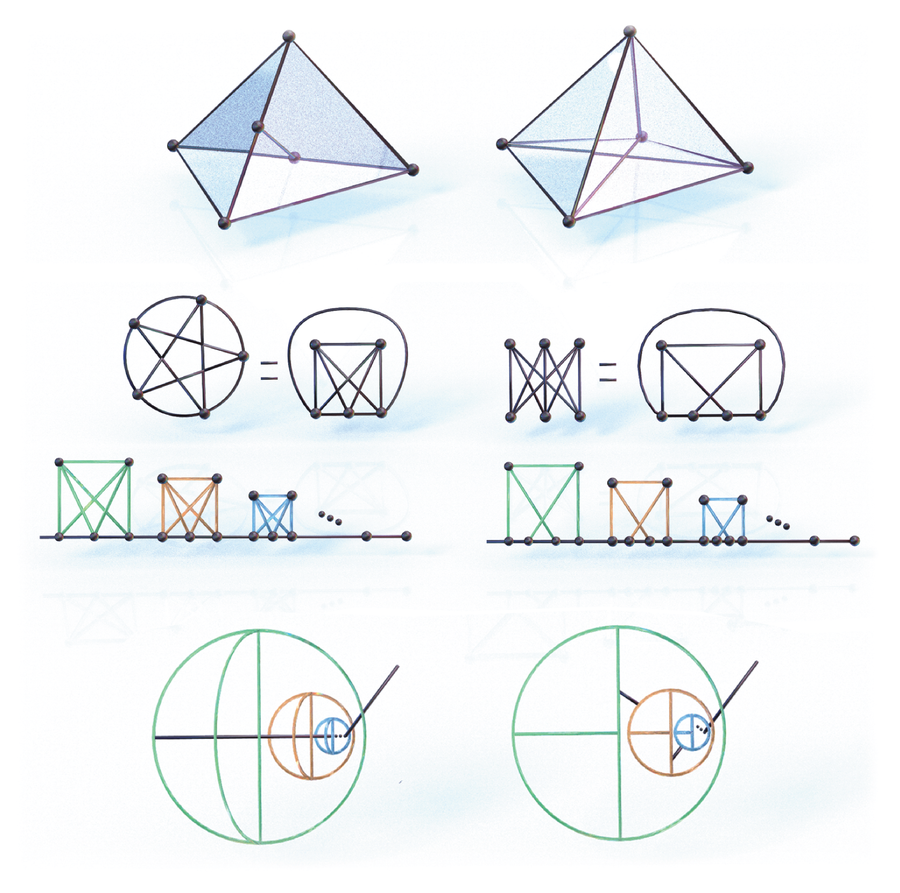
These shapes have amazing ramifications in classical topology. A topological image of a curve (shape) is a set of points in the plane that satisfies an equation and has a complicated topological structure.

The shapes shown here come from a 1930 paper by Polish mathematician Kazimierz Kuratowski. In it, he discusses peanian continua, which are, roughly speaking, simple closed curves in the plane or Euclidean 2-sphere. A simple closed curve is a continuous curve that doesn’t intersect with itself and ends at the same point where it started. Some examples of simple closed curves are shapes represented by circles, ellipses, squares and regular polygons. Kuratowski proved that a peanian continuum containing only a finite number of simple closed curves is homeomorphic [topologically equivalent] to a subset of the plane if and only if it does not contain a topological image of either curve 1 or curve 2. Generally, a homeomorphism results from a continuous deformation of the object (shape) into a new shape, thus possessing similarity of form.

William W. S. Claytor was the third African American to earn a Ph.D. in mathematics. In his 1933 doctoral dissertation, Claytor describes a more general problem that built on Kuratowski’s 1930 theorem. That problem is “the characterization of the peanian continua which are homeomorphic with a subset of the surface of a sphere.” His dissertation research moved from the case of the Euclidean plane to that of the Euclidean 2-sphere. The Euclidean 2-sphere is similar to a basketball in that it is hollow in the middle. Claytor began his problem by focusing on curves 1 and 2. Whereas Kuratowski had restricted the peanian continua to those containing only a finite number of simple closed curves, Claytor imposed no such restriction. —Asamoah Nkwanta, Morgan State University

3D Representation of Ribbon Knots

I find the three-dimensional representation of 4D objects called ribbon knots very cool. Here’s how such a representation is constructed: Take a finite collection of disks, cut slits into them, then add bands between the boundaries of the disks that are allowed to pass through these slits. If the boundary of the resulting picture is a single piece of knotted string, the result is what’s called a ribbon disk, and a knot in 3D that bounds such a disk is called a ribbon knot. In the 4D space, which we think of as surrounding the 3D space, there is enough room to undo the insertion and recover a disk (without the slits). Therefore, a ribbon knot is an example of the simplest possible type of knot in 4D, and the process of making a ribbon disk gives us a 3D way to construct it. The slice-ribbon conjecture, a major open problem in low-dimensional topology, says every such simple knot in 4D comes from a ribbon disk. I find the shape fascinating because it is a simple construction that underlies a difficult—and impossible to fully visualize—process in 4D space. Because there is more room than in 3D space, a set of points in 4D that itself constitutes a disk may occupy the space in intricate ways when we view its projection in 3D. —Christine Ruey Shan Lee, Texas State University

Cycloid

The greatest mathematical ideas have three qualities: they are simple to define, they have beautiful and surprising properties, and they generalize in interesting ways. My favorite shape, the cycloid, has all of these.

It arises from a natural question: If you follow a point on the rim of a wheel as it rolls along a road, what shape is traced out? More mathematically, what is the path of a point on the circumference of a circle as it rolls along a straight line? The resulting curve was named the cycloid by Galileo Galilei, and he is just one of the eminent mathematicians who have been fascinated by it (the list also includes Marin Mersenne, Pierre de Fermat, René Descartes, Blaise Pascal and Isaac Newton). Among the lovely properties of the cycloid is the fact that the area under its arch is exactly three times the area of the generating circle, and its length is exactly four times the diameter of that circle.

But the cycloid appears unexpectedly in a completely different context, the so-called tautochrone problem, which asks: Is there a curve such that a particle on the curve moving under gravity will reach the bottom in the same time no matter where on the curve it is released? The only curve that works is the cycloid. Bizarrely, it’s also the solution to another problem about motion.

The brachistochrone problem asks: Given two points A and B, with A higher than B, what shape should a wire between them be so that a particle moving along the wire under gravity will travel from A to B in the shortest possible time? The cycloid is again the answer. And it meets my final criterion for a great mathematical idea: it generalizes in interesting ways. If we can roll a circle along a line, what happens when we roll a circle along a circle? If you roll a circle along the outside of a circle of the same radius, for example, you get the cardioid curve, which crops up all over the place, from the central region of the Mandelbrot set [a set of numbers that produces a famous fractal] to the sound profile of a microphone to that strange pattern of reflected light you see in your coffee cup in the morning.

And what if you roll a line along a circle or another curve? This process results in what’s called the involute of the curve. Even here the cycloid has a fascinating property: the cycloid is the only curve that is its own involute. —Sarah Hart Birkbeck, University of London

Catenoid

The catenoid is a fascinating geometric surface obtained when a catenary curve—that is, a curve resembling the shape of a hanging chain—revolves around an axis. This surface has intrigued mathematicians because of its elegant shape and structural properties. It was discovered in 1744 by Swiss mathematician Leonhard Euler, who proved that the catenoid is a minimal surface, meaning it has the least possible area for a given boundary. This property can be beautifully observed with a soap film, which naturally forms a catenoid when stretched between two circular rings. What makes the catenoid even more special is that besides the plane, it is the only minimal surface that can be obtained as a surface of revolution [a surface created by rotating a curve once around].

Since the 18th century, catenary curves have also been a great source of inspiration in architecture because they distribute forces in a way that makes them ideal for building arches. Catenary arches can be found in many churches and cathedrals, as well as in other architectural masterpieces such as La Pedrera in Barcelona, designed by Antoni Gaudí. Gaudí, a visionary architect, embraced the catenary’s natural strength and beauty, incorporating the shape into his designs to create aesthetically stunning and structurally efficient structures. The catenoid and catenary continue to captivate mathematicians and architects with their combination of practicality and elegance. —Maria Soria Carro, Rutgers University

Borromean Rings

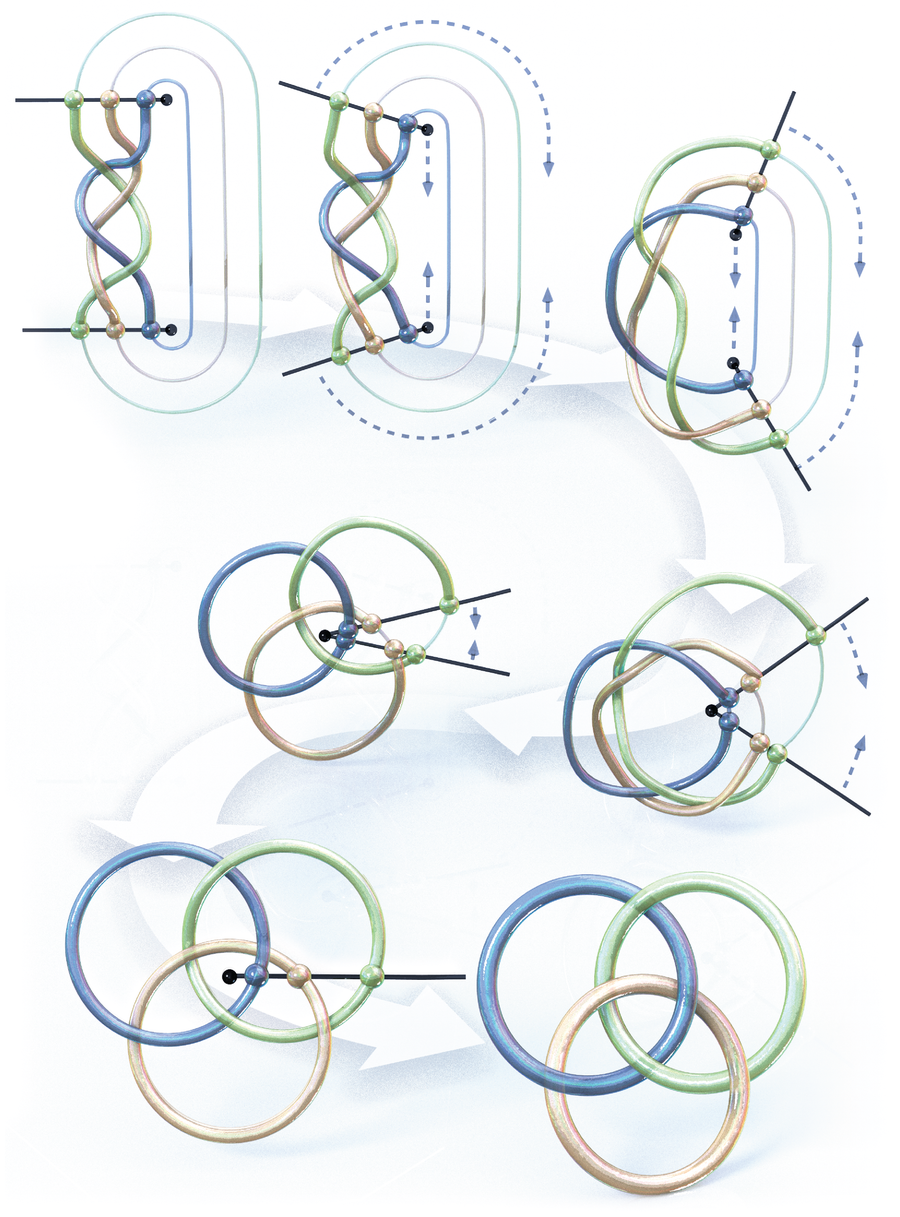
My favorite shape is probably the Borromean rings because they embody many seemingly contradictory properties all at once. The three rings are inextricably linked, yet any two are unlinked. They possess a natural symmetry yet cannot be formed from perfect circles. They offer us beauty as well as utility.

The Borromean rings can also be viewed as a “closed” braid. In this context, they provide the simplest nontrivial example of a so-called Brunnian braid, which becomes “unbraided” as soon as one strand is pulled out. It is somewhat challenging (but always possible) to form braids with this property when using four or more strands, but in fact the most familiar of all braids is Brunnian—the standard hair braid gives rise to the Borromean rings. My own research focuses on symmetries of surfaces, and Brunnian braids play a fundamental role here, arising naturally in algebraic structures that model the motion of points on a plane. —Tara Brendle, University of Glasgow